Member-only story
Numerical Surface Integrals in Python

Let’s say you wanted to calculate the area of a circle. Oh, I know the answer already, but let’s just pretend. Also, for fun suppose you want to do this numerically by breaking the circle into many tiny pieces and finding the sum of the areas of the pieces. How would you do that?
I’ll be honest. I don’t want to find the area of a circle. I want to find the magnetic flux through a circle for a complicated magnetic field. This means I’m going to use a numerical calculation to find the magnetic field at a bunch of locations and then use those to find the flux. Since the magnetic field changes over the surface of the circle, I’m going to need to do a numerical surface integral.
Surface Integral in Cartesian Coordinates
Here is the easiest option — break the surface into tiny squares with the dimensions of each square as dx by dy. Yes, this assumes the circle is in the x-y plane. Here is a diagram.
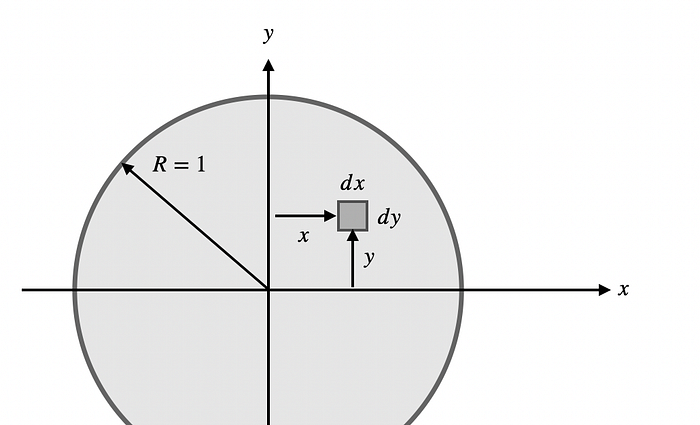
The area of this square is
So, if you break this area into N number of squares, the total area would be NdA. Simple, right? Well, sort of. The problem is finding the total number of blocks to add up. OK, how about some numbers? If this circle has a radius of 1 (I left off the units because it doesn’t matter right now). The distance from one side to the other along the x-axis is 2 units. Now suppose I have tiny blocks that are 0.2 by 0.2. I’m going to use finite sized squares because I want to do a numerical calculation. In calculus, you would take the limit as the block sizes go to zero. But in this finite square case, how many of these would fit across the circle?

Yes, the answer is 10. There should be 10 blocks across the diameter — OK, approximately 10 since the blocks don’t fit perfectly. Don’t worry about that for now though.
But what about the next row of blocks? If I add a row on top of this, it will probably need fewer than 10 blocks since the width of the circle is smaller as…
